The following technique is a spin-off of the development of an improved search engine. It enables the user to omit logical junctions like AND or OR. Furthermore it is possible to do fuzzy queries, that means, a user can put in "roof window chimney door room" if he's searching for documents that contain "house".
In the context of this article fuzzyness does not mean that a word may contain misspellings or different notations; instead, it is meant that a user can circumscribe the semantic of one word by a couple of other words.
The human brain works with associations. Given a concept, a person remembers to others automatically, for example:
clock - time - season - spring - flower - bee - insect - animal.
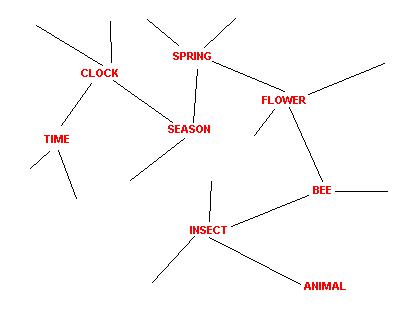
Such associative chains can be depicted as a graph, a semantic network. Each symbol is a unique vertex and each association between two symbols an edge. In AI applications of semantic networks often labelled edges can be seen. That doesn't play a role here, all edges be unnamed.
Def.: the semantic distance between two symbols is the least count of edges in an associative graph that must be passed to get from one symbol to the other. Especially a symbol has the semantic distance of 0 to itself.
In the domain of fuzzy logic, propositions have a truth value that may not only be 0 or 1, but as well any number between. For example 0.1 means "nearly false", 0.5 means "half true, half false". The operators NOT, AND and OR are generalized this way: NOT(x) is 1-x, AND(x,y) is min(x,y) and OR(x,y) is max(x,y).
Def. Fuzzy-similarity(sym1,sym2) := (maxD-d)/maxD where sym1 and sym2 are symbols in a semantic net, d is the distance between them and maxD is the highest allowed semantic distance. If the given symbols have a higher distance in the graph, the distance is defined as = maxD.
Comment on maxD: it turned out that between two concepts within a semantic net two intermediate symbols can be assumed, so maxD can be set in most cases to 3.
Every symbol in the graph is assigned a number between 0 and 1 with respect to the start symbol. If we have two different start symbols, every symbol in the graph is assigned a pair (a,b) of numbers with a and b element of [0.0 .. 1.0]. Now we're able to apply the operators of the fuzzy logic, min for the and operator and max for the or operator.
Example: let's take the symbols clock and animal in the following one-dimensional net as start symbols. max be 6 here. The usage of a maximum semantic distance does only serve to put a limit upon the necessary amount of computation, because the semantic net might be very big.
Clock - Time - Season - Spring - Flower - Bee - Insect - Animal
For the distances regarding clock we get the list of pairs:
| Clock | Animal |
-----------+--------+--------+
Clock | 0 | 6 |
Time | 1 | 6 |
Season | 2 | 5 |
Spring | 3 | 4 |
Flower | 4 | 3 |
Bee | 5 | 2 |
Insect | 6 | 1 |
Animal | 6 | 0 |
|
Transformed by the term (maxD-d)/maxD into fuzzy truth values:
| Clock | Animal |
-----------+-------+--------+
Clock | 1.00 | 0.00 |
Time | 0.83 | 0.00 |
Season | 0.67 | 0.17 |
Spring | 0.50 | 0.33 |
Flower | 0.33 | 0.50 |
Bee | 0.17 | 0.67 |
Insect | 0.00 | 0.83 |
Animal | 0.00 | 1.00 |
|
Verwendet man die Minimum-Funktion für das Fuzzy-UND und die Maximum-Funktion für das Fuzzy-ODER, so ergibt sich:
| Clock | Animal | Clock AND Animal | Clock OR Animal |
-----------+-------+--------+------------------+-----------------+
Clock | 1.00 | 0.00 | 0.00 | 1.00 |
Time | 0.83 | 0.00 | 0.00 | 0.83 |
Season | 0.67 | 0.17 | 0.17 | 0.67 |
Spring | 0.50 | 0.33 | 0.33 | 0.50 |
Flower | 0.33 | 0.50 | 0.33 | 0.50 |
Bee | 0.17 | 0.67 | 0.17 | 0.67 |
Insect | 0.00 | 0.83 | 0.00 | 0.83 |
Animal | 0.00 | 1.00 | 0.00 | 1.00 |
|
Remark: the NOT function is not considered here. The method shall work without the use of operators like 'not' or '-'.
Fuzzy logic can be used to assign numbers zu symbols. These numbers can be used to evaluate documents. A method will be shown that refrains from the use of logical operators. The user is simply required to put in a list of search keywords.
After the user puts in a query, in a first step for each keyword a list of associated words is gathered from the graph. Since the graph may be very big, one must restrict to a certain maximum length of the list and a maximum semantic distance. Each word of the list is stored together with its semantic distance to the keyword.
Example: suppose, the user types into the search engine's query interface: elephant, cakefork, spoon, rhino
Then anyone's semantic net might yield the following associations. The length of the list(s) is restricted to 8. The maximum semantic distance be 10 here.
Elefant (0) | Kuchengabel (0) | Kaffeelöffel (0) | Rhinozeros (0) ---------------+-----------------+------------------+--------------- Dickhäuter (1) | Gabel (1) | Kaffee (1) | Dickhäuter (1) Nilpferd (1) | Löffel (2) | Tee (2) | Elefant (1) Nashorn (1) | Messer (2) | Teezeremonie (3) | Rüssel (2) Rhinozeros (1) | Gabel (2) | Japan (4) | Schlauch (3) Krokodil (2) | schneiden (3) | China (5) | Feuerwehr (4) Nil (2) | schnitzen (3) | Peking (6) | Fahrrad (4) Ägypten (3) | Holz (4) | Pagode (7) | Wettrennen (5) Afrika (4) | Bildhauer (5) | Turm (8) | Autorennen (6) |
Elephant (0) | Cakefork (0) | Kaffeelöffel (0) | Rhino (0) ---------------+-----------------+------------------+--------------- Pachyderm (1) | Fork (1) | Coffea (1) | Pachyderm (1) Nilpferd (1) | Spoon (2) | Tea (2) | Elephant (1) Nashorn (1) | Knife (2) | Tea Ceremony (3) | Trunk (2) Rhino (1) | Fork (2) | Japan (4) | Hose (3) Crocodile (2) | cut (3) | China (5) | Fire Brigade (4) Nil (2) | carve (3) | Beijing (6) | Bicycle (4) Egypt (3) | Wood (4) | Pagoda (7) | Race (5) Africa (4) | Sculptor (5) | Tower (8) | Car Race (6) |
Nun werden mit herkömmlichen Suchmaschinen-Methoden Dokumente gesucht, die irgendeines der Symbole in irgendeiner dieser Listen enthalten. Für jedes der Suchworte wird für das betreffende Dokument gemerkt, was die jeweilige minimale semantische Distanz des Dokumentes zum Suchwort ist.
The next step is to use traditional search engine methods to retrieve documents that contain any of the symbols in the table.
Beispiel: wenn das Dokument die Worte Löffel, Holz und Bildhauer enthält, so ist die Distanz zum zweiten Suchwort = 2, weil Löffel sowohl im Dokument vorkommt als auch den geringsten semantischen Abstand zu Kuchengabel besitzt.
Nehmen wir an, ein Dokument bestünde aus den Worten {Elefant, Tee, Turm, Schlauch}. Es ergeben sich dann folgende semantische Distanzen der Suchworte zum Dokument (dd genannt):
Suchwort | dd -------------+----- Elefant | 0 Kuchengabel | 10 Kaffeelöffel | 2 Rhinozeros | 1 |
Man beachte, daß die Distanz des Dokuments zu Kuchengabel 10 ist, weil keines der mit Kuchengabel assoziierten Symbole im Dokument enthalten ist. Hier wird das (willkürlich gewählte) Maximum eingesetzt.
Note that the distance zu-tun
Auf diese Weise ergeben sich für sämtliche Dokumente jeweils n-Tupel (n ist hier die Anzahl der Suchworte). Diese Tupel kann man nun zum Bilden einer Bewertungszahl (Rang) heranziehen.
For example one could sum up all components of the n-tuple or their squares.
Das wäre aber eine Vorgehensweise, die den Nachteil hätte, daß Suchworte, die einfach nur wiederholt werden, mit zu hoher Gewichtung in die Dokument-Bewertung einfließen.
Another disadvantage is that this method would not recognize groupings within the query words.
Let's take the following query as example
collie terrier dachshund poodle building dwelling roof
Es ist offensichtlich, daß es sich hier um zwei semantische Cluster handelt, nämlich "Collie Terrier Dackel Pudel" und "Gebäude Wohnung Dach". Entsprechend sollten semantische Distanzen zu Mitgliedern der Cluster jeweils nur ein einziges Mal gewertet werden.
Obviously these are two semantic clusters: "collie terrier dachshund poodle" and "building dwelling roof". According to the fact that each cluster may contain an arbitrary number of items, the occurrence of any member of a cluster in a document should be counted once for this cluster.
Eine Möglichkeit, diesem Problem zu begegnen, ist, in der Berechnung der Bewertungszahl eines Dokumentes die paarweise semantische Distanz zwischen den Suchworten zu berücksichtigen. Angenommen, die Suchwörter hießen S1, S2, ... Sn. Wenn man die paarweisen Komponenten der Distanzvektoren aufaddiert, so kann man dies auffassen als die Berechnung von f(S1 op S2) + f(S1 op S3) + ... f(S(n-1 ) op Sn) op ist hier eine fuzzylogische Operation. Diese sollte wegen Forderung F2 abhängen von der der semantischen Distanz der Suchworte untereinander. Das heißt, je näher ein Paar von Suchworten Si und Sj semantisch beieinander liegen, desto ODER-artiger sollte die Operation sein, und je weiter semantisch entfernt die Suchworte liegen, desto UND-artiger sollte die Operation aussehen.
One countermeasure for this problem is to consider each pair of query words to calculate the rank of a document from. Suppose the words of the query were S1, S2, ... Sn. zu-tun
This can be reached by a linear combination of the OR and the AND value.
If ds is the semantic distance between two keywords of a query in regard to a semantic net, one gets a normalized distance value dn as (maxD-ds)/maxD.
At ds = 0, dn is = 1. At ds = maxD, dn is = 0. When the semantic distance is low, the OR term should be given more weight. When the semantic distance of a pair of symbols is high, the AND term should be given a higher weight. dn is a real number between 0 and 1.
For two components dd1 and dd2 of the distance vector the AND part is max(dd1,dd2) and the OR part is min(dd1,dd2). dd1 and dd2 are semantic distances of one document to two of the query words S1 and S2.
Now we must take the semantic distance among each pair of the words of the query into account. According to this distance we choose a point between min(dd1,dd2) and max(dd1,dd2).
In order to evaluate a document for a given query, determine for each of the words in the query the least semantic distance dd1, dd2, ... ddn to the document. For each pair (ddi, ddj) with i < j sum up this expression:
f := max(ddi,ddj) - (maxD - ds)/maxD * (max(ddi,ddj) - min(ddi,ddj))
This means: if two keywords of a query are very far apart from each other in a semantic sense, then ds is big and the term (maxD-ds)/maxD is near to 0. In this case the bigger distance component max(ddi,ddj) counts for the result of f. If the current keyword pair consists of symbols with a small semantic distance, then (maxD - ds) / maxD is near to 1. Then the term min(ddi,ddj) has the biggest influence on f.
The described method needs a semantic network. It must normally be gathered and put in by the user, because, if a document addresses interdisciplinary interests, the person that adds keywords to a document would likely invent a new symbol not mentioned in the text.
Flections are not considered in the described algorithm. If a person searches for 'goose', documents that contain 'geese' only can't be retrieved. A countermeasure against this odd is to put in additional keywords when a document is stored, especially stem forms of the keywords. In most cases, authors of documents know this problem and provide such keywords, for example in the case of HTML, in meta tags.
Queries with many keywords are computational very expensive. But is possible to parallelize them. For example, if the search were internet-wide, one could retrieve query results from different search engines at the same time. Another possibility for parallelization would be to launch several search processes on the same search engine.